The Digits: 0-9 and A-F
Hexadecimal is a base-16 number system. That means there are 16 possible digits used to represent numbers. 10 of the values are numerical and the same as used in the decimal system (0, 1, 2, 3, 4, 5, 6, 7, 8, and 9). Also these values represent the same value you’re used to. The remaining six digits are represented by A, B, C, D, E, and F, which map out to values of 10, 11, 12, 13, 14 and 15.

People use both upper and lower case representations of A-F. Both work and there isn’t much of a standard in terms of upper versus lower case. A3F is the same number as a3f, which is the same number as A3f.
Subscripts
Decimal and hexadecimal have 10 digits in common, so they can create some similar looking numbers. However, 10 in hex is a different number from that in decimal. Hex 10 is equivalent to decimal 16. We need a way to show whether a number we’re talking about is base 10 or base 16 Enter base subscripts:
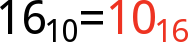
Hexadecimal 10, indicated by a subscript 16, is equivalent to decimal 16 (notice the subscript 10).
As you’ll see further down, subscripts aren’t the only way to explicitly state the base of a number. Subscripts are just the most literal system we can use.
Counting in Hex
Counting in hex is a lot like counting in decimal, except there are six more digits to deal with. Once a digit place becomes greater than “F”, you roll that place over to “0”, and increment the digit to the left by 1.
Let’s do some counting: